Number Theory Solver app for iPhone and iPad
Developer: shane mulligan
First release : 11 Jan 2015
App size: 820 Kb
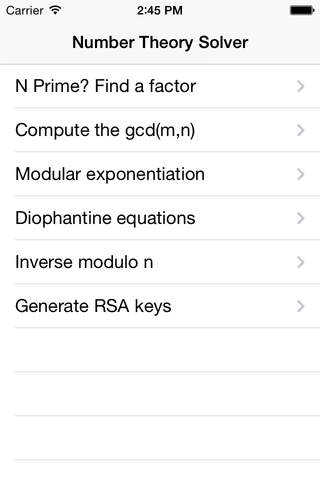
This app performs 6 fundamental calculations in number theory. These form a basis for many algorithms in cryptography and computer security. They are:
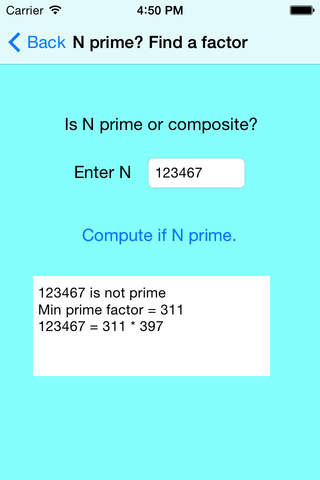
1. Determine if number is prime, or find the smallest prime factor if it is not prime. This can be used repeatedly to find all the prime factors of a number.
2. Find the gcd (greatest common divisor) of two integers, i.e. the largest integer that divides both numbers.
3. Compute a number mod n, (modular arithmetic), or a number raised to a power mod n, i.e. modular exponentiation a^b mod n. For example 2^50 mod 15.
4. Find the integer solutions x and y to Diophantine equations, i.e. equations of the form ax + by = c, where a, b, c are all integers.
5. Compute the modular inverse. Solve ax = 1 mod n, for integer x, given integers a and n.
6. Generate the RSA public and private keys, given two primes p and q.
Please submit your comments and suggestions to improve this app for future versions.
Email: shane.mulligan at dit .ie